| | EL LENGUAJE
MATEMÁTICO |
“El lenguaje matemático es el único lenguaje universal” (Alain Connes)
“Es común hablar de ‘el lenguaje de las matemáticas’. ¿Pero es la matemática verdaderamente un lenguaje?” (F. David Peat)
“Para interpretar la notación matemática es preciso conocer qué clase de gramática usa” (Stephen Wolfram)
El Problema del Lenguaje Matemático
Se considera que la matemática tiene un lenguaje propio, un lenguaje abstracto y diferente del lenguaje natural:
“La naturaleza está escrito en el lenguaje de las matemáticas y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es humanamente imposible entender una sola palabra de él; sin esto, uno se encuentra perdido en un oscuro laberinto” (Galileo, en “Il Saggiatore”, El Ensayador, 1616).
Este planteamiento de Galileo fue realmente revolucionario en su época, al sustituir el concepto antiguo de naturaleza como una organización superficial y concreta de sustancias materiales por una estructura profunda y abstracta, la proporcionada por la matemática.
¿Pero realmente existe un lenguaje matemático? Podemos afirmar que no existe porque la matemática no tiene un lenguaje formal. Solo tiene algunos símbolos básicos de tipo abstracto que se han ido creando a lo largo de la historia, y en los que existe consenso general. Los más importantes son:
Símbolos numéricos:
0 … 9 + − × · ÷ / √ ∞ π e Φ i ∑ Π ∫
Símbolos de comparación:
= ≠ < > ≥ ≤ ≡
Símbolos de la teoría de conjuntos:
∅ ∩ ∪ ⊃ ⊇ ⊈ ⊂ ⊆ ∈ ∉ { }
Símbolos lógicos:
∀ ∃ ¬ ∧ ∨ → ↔
De todos estos símbolos, los dígitos 0 a 9 son el fundamento del lenguaje numérico, un lenguaje verdaderamente universal que forma parte de nuestra vida diaria. “Las cifras constituyen hoy el único y auténtico lenguaje universal” (Georges Ifrah).
La potencia de la matemática moderna reside en sus símbolos, que encapsulan o compactan conceptos precisos. Sin embargo, en matemática, cualquiera es libre de usar cualquier notación, siempre que la explique. El hecho real es que la notación matemática no es universal, pues se interpreta de manera diferente según el tema, el autor e incluso el contexto.
Entre las carencias de la matemática en su aspecto lingüístico están las siguientes:
Falta de gramática
La matemática carece de lenguaje formal porque carece de gramática. Se suele afirmar que la notación matemática no es problema matemático, que es un problema lingüístico, pero no es cierto, porque los conceptos fundamentales o primitivos de la matemática deberían reflejarse en la semántica del lenguaje matemático, junto con su correspondiente sintaxis.
Mezcla con el lenguaje natural
No hay un lenguaje matemático puro, pues está mezclado con el lenguaje natural, es decir, se apoya en el lenguaje natural. Un ejemplo es la definición de la estructura matemática de grupo, que se define de la siguiente manera:
- Hay un conjunto G.
- Hay una operación interna binaria (simbolizada por "*") definida sobre G, es decir, para todo par de elementos, x e y de G, x*y es un elemento de G: x*y∈G.
- Existe un elemento e (llamado neutro) tal que x*e = e*x = x para todo elemento x de G.
- Para todo elemento x de G, existe otro elemento x' (llamado “inverso de x”) tal que x*x' = x'*x = e
- Los elementos de G cumplen la propiedad asociativa: x*(y*z) = (x*y)*z.
El problema es que el lenguaje natural es ambiguo, es decir, admite muchas interpretaciones.
Un avance hacia al lenguaje matemático puro fue la aparición del álgebra, en donde se utilizan letras (que representan variables) para liberarse de la esclavitud de la palabra. La utilización de símbolos en álgebra representó un gran salto cualitativo, abriendo una nueva era en la matemática.
Polimorfismo
En el lenguaje matemático hay polimorfismo, es decir, que la semántica de algunos operadores varía en función de los argumentos. Se dice que los operadores tienen “sobrecarga” semántica. Por ejemplo:
- Las operaciones de suma y resta de vectores y matrices utilizan los mismos símbolos que la suma y resta de números.
- La operación de restar conjuntos está representada por el mismo símbolo que el de restar números.
- La notación exponencial. En este caso, el polimorfismo está agravado por el hecho de que no hay operador explícito. En efecto, la notación xn puede significar (dependiendo de la naturaleza de la base): potencia numérica, potencia cartesiana, potencia de matrices, e incluso aplicación n veces de una función. En todos estos casos, el exponente indica repetición n veces sobre el argumento (base) de una operación que hay que inferir por el contexto.
En el caso de que el exponente sea −1, puede significar número inverso, matriz inversa o función inversa.
Bidimensionalidad
La sintaxis del lenguaje matemático es bidimensional, que tiene la virtud de la legibilidad porque está pensado para el consumo humano, pero tiene el inconveniente de que no sirve para tratamiento informático (o es muy difícil), pues se requiere linealidad. La bidimensionalidad aparece en la notación exponencial, en los superíndices y subíndices, en las matrices, en operaciones como sumatorio y productorio, en las integrales definidas entre dos límites numéricos, etc.
La bidimensionalidad más frecuente es la notación exponencial. Esta notación se considera un avance muy importante en matemáticas. Intuida por Napier, fue Descartes quien generalizó la práctica de escribir “potencias” tal y como lo hacemos hoy día. Así, x3 sustituye a x·x·x. Descartes hizo pública esta notación junto con otros perfeccionamientos del álgebra en el tercer apéndice (la Geometría) de “El Discurso del Método” en 1637. La notación incluye dos niveles: base y exponente. Este último se expresa con un símbolo más pequeño. Cuando hay más de dos niveles hay graves dificultades de representación.
La codificación numérica
El sistema decimal de representación numérica está firmemente asentado en nuestra cultura y es considerado uno de los grandes avances conceptuales de la historia de la humanidad. Pero desde un punto de vista lingüístico y combinatorio, no es suficientemente genérico:
- No hay posibilidad de que un número pueda expresarse mediante otros números y no sólo dígitos. Por ejemplo, la codificación 2(−15)7 consta de tres números, siendo el segundo un número negativo de dos dígitos. Una interpretación de tipo posicional podría ser 2×102 − 15×10 + 7 = 57.
En Matemática Védica se utiliza una versión restringida de este sistema, pues se admite el “signo posicional” sobre un dígito. Por ejemplo, 329 se interpreta como 3×102 − 2×10 + 9 = 289.
- La codificación numérica se basa en los llamados "valores de posición", que son potencias de base 10. No hay ninguna razón para que estos valores de posición puedan ser también cualquier número, siempre que siga un patrón genérico. Por ejemplo, desde el punto de vista computacional, es más adecuado utilizar el sistema de Cantor, que permite representar cualquier número racional p/q de forma exacta mediante una secuencia finita y, por lo tanto, sin pérdida de precisión. Por ejemplo, un número tan sencillo como el racional 1/3 es 0,33333... tiene infinitas cifras decimales, por lo que, sin ser un número irracional, no se puede “capturar” mediante una representación finita. Lo más lógico sería utilizar el sistema de Cantor. [ver Aplicaciones – Matemática – La Paradoja 1 = 0,999…]
Otra forma de representación exacta de números racionales es mediante fracciones continuas [ver Aplicaciones – Matemática – Fracciones Continuas].
Gap semántico. Deshumanización y complejidad
Existe una brecha entre la matemática y la forma humana de pensar. La matemática, en su forma actual, no es humanista. Es un lenguaje críptico, poco natural e intuitivo, orientado solo para especialistas o iniciados.
- A nivel sintáctico, la matemática ha desarrollado un lenguaje críptico, difícil de entender, deshumanizado. “La notación matemática está llena de signos y símbolos que la gente normalmente no usa y que la mayoría de la gente no entiende” (Stephen Wolfram).
- A nivel semántico, la matemática no refleja claramente el significado, o bien lo olvida o lo elimina, pues es a veces ciega, mecánica, de mero cálculo, cuando debería ser una forma de descripción y manipulación del significado. El cálculo no debe ser ciego, sino debe expresar la semántica tanto del problema como de los pasos asociados con la solución.
Este gap lingüístico puede conducir a una cierta deformación o deterioro mental.
- “La matemática produce daños en la conciencia por la separación, por las fronteras, por no percibir y trabajar con la conciencia unificada” (Ken Wilber).
- “No cabe duda de que la prolongada dedicación a ejercicios matemáticos en economía conduce a la atrofia del juicio y de la intuición” (John Kenneth Galbraith).
Todo esto ha provocado que la matemática sea percibida como una disciplina abstrusa y distante de la realidad cotidiana. Y el aprendizaje de la matemática como una actividad pesada, difícil y artificial, poco natural y deshumanizada.
Limitaciones expresivas
La notación matemática adolece de graves limitaciones expresivas, incluso las más elementales, que, por otra parte, sí disponen los lenguajes informáticos.
Si hay limitaciones expresivas en lo simple, más problemas hay con los fenómenos complejos que no pueden modelizarse con la matemática tradicional como sistemas distribuidos, sistemas cliente-servidor, sistemas compartidos, etc., así como para expresar paradigmas de programación como: programación orientación a objetos, a eventos, a agentes, a aspectos, programación genérica, evolutiva, multidimensional, etc. Tampoco hay un formalismo para los mecanismos de paralelismo, concurrencia o sincronización, como en los lenguajes informáticos.
Es precisamente por estas limitaciones expresivas de la matemática que tuvieron que inventarse los lenguajes informáticos. Si el lenguaje matemático hubiera sido suficientemente potente en este sentido, no habría habido necesidad de inventar tantos lenguajes informáticos, una autentica torre de Babel.
También hay limitaciones expresivas que impiden describir los fenómenos de la física cuántica, entre ellos:
- Superposición de estados.
Consiste en que una propiedad de una partícula cuántica posea varios estados a la vez, aunque al realizar una medida se fuerza a la partícula a que pase a uno de los estados de superposición (postulado de proyección).
- Entrelazamiento cuántico.
Consiste en que dos partículas (electrones, neutrones, fotones) que han compartido alguna vez una misma propiedad (por ejemplo, el espín) permanecen interconectadas, por muy alejadas que estén entre sí, incluso millones de kilómetros, de tal forma que un cambio en una de ellas produce instantáneamente un cambio en la otra.
- Ubicación múltiple o difusa de una partícula.
Una partícula (por ejemplo, un electrón) está simultáneamente en varios sitios a la vez.
- Saltos instantáneos de una entidad cuántica en el espacio. Por ejemplo, un electrón salta de una órbita a otra sin pasar por espacio intermedio. O el salto instantáneo de una entidad cuántica por una barrera de potencial.
Falta de lenguaje algorítmico
La notación matemática tradicional permite representar objetos matemáticos, pero no procesos matemáticos. Muchos matemáticos afirman que la matemática solo trata de demostraciones formales. Desde este punto de vista, la computación no tiene cabida en matemáticas.
Por lo tanto, no existe un lenguaje canónico (o estándar) para representar algoritmos. Se suele utilizar una especie de pseudocódigo (informal), mezcla de lenguaje formal y natural. Se habla de una nueva disciplina: la “matemática computacional”, una matemática que trata con algoritmos y su experimentación.
¿Es la informática diferente de la matemática o parte de ella? Según Donald Knuth, “Las matemáticas tratan de teoremas, procesos infinitos y relaciones estáticas, mientras que la informática trata de algoritmos, construcciones finitas y relaciones dinámicas”. Sin embargo, el concepto de algoritmo debería ser uno de los conceptos centrales de la matemática.
Al no existir dinamicidad, no existe el tiempo en matemáticas. Esto es lógico, porque el tiempo es un concepto físico. Pero también el espacio es un concepto físico y, sin embargo, la matemática trata con espacios abstractos. Por lo tanto, debería haber también “tiempo abstracto”.
Confusión entre igualdad, sustitución y equivalencia
Decir que una cosa es igual a sí misma es una obviedad (una tautología), que no añade conocimiento. Y decir que dos cosas son iguales es una contradicción. En este segundo caso, es mejor decir que existe equivalencia entre ambas, como cuando expresamos que la suma es conmutativa: x+y ≡ y+x, que hacen referencia a lo mismo. En este sentido, Frege distinguía entre sentido (la forma de expresión) y referencia (el objeto referenciado por la expresión). Puede haber muchos sentidos equivalentes asociados a la misma referencia.
Ejemplos:
- La expresión x+0 = x interpretada como ecuación nos da (restando x de ambos lados) 0 = 0. Interpretada como cálculo, indica que la suma de x y 0 es 0.
- La expresión i2 = −1 debe interpretarse, no como una ecuación, sino como una sustitución. Por lo tanto:
- No es cierto que i sea la raíz cuadrada de −1.
- i debe interpretarse como una entidad matemática tal que su cuadrado es −1.
- Cuando en una expresión aparezca i2, se sustituye por −1.
- La expresión ε2 = 0, que define un infinitésimo, debe interpretarse también como una sustitución, porque si fuera una ecuación, se deduciría que ε = 0.
- La definición de la proporción aúrea es Φ = 1 + 1/Φ.
Como igualdad, es una ecuación, cuya solución es Φ = (√5 + 1)/2
Como sustitución, es una expresión recursiva:
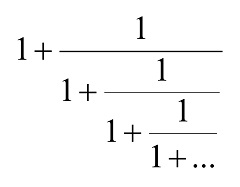
La sustitución es la operación clave que nos permite definir expresiones imaginarias en general, incluyendo los números imaginarios, el infinito y el infinitésimo. En este sentido, la sustitución es el “puente matemático” que permite conectar lo real y lo imaginario.
También hay confusión entre igualdad y equivalencia. Por ejemplo, las fórmulas de física f = m·a y E = m·c2 no son igualdades (aunque se diga p.e. “fuerza igual a masa por aceleración”) sino que se trata de equivalencias.
“Decir de dos cosas que son iguales es insensato, y decir de una cosa que es igual a sí misma es inútil” (Wittgenstein). En este sentido, la igualdad no tiene sentido; solo tienen sentido la sustitución y la equivalencia.
Confusión entre parámetros y argumentos de una función
Hay poca claridad entre la definición de una función (con sus parámetros) y la aplicación de la función (con sus argumentos). En definitiva, que no hay clara diferencia entre argumentos y parámetros. Dada una expresión aislada, no se sabe si las variables son argumentos o parámetros. Este problema fue abordado por Alonzo Church en su cálculo lambda [ver Comparaciones – MENTAL vs. Cálculo Lambda.]
Magnitudes
La matemática no contempla el concepto de magnitud, algo tan común en la vida cotidiana y en física. Una magnitud se compone de un número (cantidad) y una unidad. Por ejemplo, en lenguaje coloquial decimos, por ejemplo, “3 naranjas”. Sin embargo:
- Debería haber un símbolo, un formalismo que conecte cantidad con unidad.
- Debería poderse operar con magnitudes y entre magnitudes.
- Las funciones deberían poder utilizar magnitudes como argumentos o como resultado.
- La unidad debería poder ser cualquier entidad matemática y no solo entidades físicas.
Operadores aritméticos de orden superior
En aritmética están definidos los operadores de suma, producto y potencia, así como sus inversos. Pero se necesita una notación estándar que permita expresar también las potencias de orden superior y sus inversas.
División por cero
Se dice que el resultado de la expresión 0/0 es “indeterminada”, es decir, que puede ser cualquier número. Pero esto no es admisible. Necesitamos una expresión que sea el resultado, pues si no, la matemática es incompleta desde el punto de vista operativo. Lo mismo ocurre con la expresión 1/0, que se dice que su resultado es “infinito”.
Paralelismo
Este concepto, tan habitual en informática, no existe en matemática. Se refiere a que varios procesos se ejecutan (o evalúan) en paralelo, pero también puede hacer referencia (o aplicarse) a la existencia de varias entidades matemáticas que se presentan simultáneamente, como la concurrencia de varios estados en física cuántica.
MENTAL, un Lenguaje Matemático
Con MENTAL se resuelven y aclaran estos problemas asociados al lenguaje matemático:
- Gramática.
El lenguaje matemático no puede ser un lenguaje concreto, con una gramática sintáctica particular, porque eso sería limitar a la matemática. La matemática es esencialmente libertad y creatividad. “La esencia de la matemática reside en su completa libertad” (Cantor). Un lenguaje matemático debe tener una gramática semántica, es decir, una gramática basada en conceptos generales y la combinatoria de dichos conceptos, que representan grados de libertad, para poder expresar todo tipo de ideas creativas. Esta gramática semántica es la de MENTAL. El desarrollo de la matemática está ligado al lenguaje matemático. Un lenguaje basado en conceptos abstractos y genéricos facilita la creatividad.
Es lo mismo que ocurre con el tema del modelo de la mente. No puede haber un modelo específico de la mente porque la mente tiene grados de libertad, que son las primitivas semánticas universales y los mismos recursos que la gramática semántica de MENTAL.
La falta de un lenguaje matemático estándar es reflejo de su falta de fundamentación. En MENTAL, lenguaje y fundamentación van unidos. Las primitivas semánticas universales constituyen el lenguaje y son el fundamento de la matemática.
MENTAL es un lenguaje matemático que abre la conciencia, que proporciona libertad y proporciona una visión profunda de la unidad subyacente de todas las cosas.
Un lenguaje particular refleja una cultura y su historia, una identidad y una forma específica de ver el mundo. El lenguaje matemático tiene que ser transcultural y universal por su propia naturaleza. Y esa universalidad la proporcionan los universales semánticos, las primitivas de la gramática semántica.
Según Chomsky, existe una gramática universal innata y común a todos los seres humanos. Aquí defendemos que esta gramática universal se basa en las primitivas semánticas universales (o arquetipos primarios) de MENTAL, que son comunes a mente y naturaleza.
- Mezcla con el lenguaje natural.
MENTAL es un lenguaje formal “puro”, completo y autosuficiente. No necesita del lenguaje natural. Es un lenguaje con semántica y sintaxis perfectamente definidas. Es como un lenguaje de programación de ordenadores.
- Polimorfismo.
En MENTAL no hay polimorfismo con sobrecarga. Toda operación tiene una semántica precisa y fija, donde los argumentos pueden ser de cualquier tipo. Solo que si la operación no puede realizarse, la expresión correspondiente se autoevalúa.
- Bidimensionalidad.
Este problema desaparece porque MENTAL es unidimensional. Por lo tanto puede ser tratado informáticamente.
- La codificación numérica.
La codificación numérica es genérica en el sentido de que todo componente de una secuencia puede ser cualquier número o expresión.
>Gap semántico. Deshumanización y complejidad.
En MENTAL no hay brecha semántica. Las primitivas semánticas son conceptos de sentido común, sencillos, claros y comprensibles. Por lo tanto, es un lenguaje humanista. “La mayoría de las ideas fundamentales de la ciencia son esencialmente simples, y pueden, como regla, ser expresadas en un lenguaje comprensible para todos” (Einstein).
- Limitaciones expresivas.
Con MENTAL se pueden expresar todo tipo de relaciones, incluso las más extrañas de la física cuántica.
- Falta de lenguaje algorítmico.
MENTAL es un lenguaje operativo, procedimental u algorítmico. Toda expresión es evaluada y produce un resultado (que puede ser la propia expresión). MENTAL es un lenguaje válido para la matemática y la informática. La frontera entre estas disciplinas se difumina.
- Confusión entre igualdad, sustitución y equivalencia.
En MENTAL estos tres conceptos se aclaran.
- Confusión entre parámetros y argumentos de una función.
En MENTAL se diferencian claramente estos dos tipos de elementos.
- Magnitudes.
Con MENTAL se pueden definir dos tipos de magnitudes: cuantitativas y cualitativas. En las primeras, la cantidad puede ser cualquier número. En las segundas, hay un factor entre 0 y 1 aplicable a una cualidad.
- Operadores aritméticos de orden superior.
Con MENTAL se pueden expresar operadores aritméticos de orden superior.
- División por cero.
En MENTAL, existen expresiones específicas para representar las expresiones 1/0 y 0/0. Por lo tanto, no se produce una excepción y el proceso puede continuar sin interrupción.
- Paralelismo.
El paralelismo se contempla simplemente con la operación de conjunción, que es aplicable a objetos o procesos.
Adenda
La importancia del lenguaje en matemática
Para André Weil, el desarrollo de nuevas ideas matemáticas es paralelo al desarrollo de nuevas formas lingüísticas. Weil creó un nuevo lenguaje matemático que le permitió expresar conceptos matemáticos que eran inexpresables con el lenguaje matemático convencional, Este lenguaje surgió dentro del grupo Nicolas Bourbaki (del que Weil fue uno de sus fundadores) de unificación de la matemática contemporánea. Las ideas de Weil se convirtieron en los fundamentos de lo que hoy denominamos “álgebra geométrica”.
Alexander Grothendieck, un gran matemático innovador del siglo XX dio vida al esquema del nuevo lenguaje creado por Weil, ideando un nuevo lenguaje matemático abstracto revolucionario para el álgebra y la geometría, que permitió a los matemáticos expresar ideas que anteriormente eran imposibles de expresar. Grothendieck escribió varios libros en los que mostraba las grandes posibilidades expresivas de su lenguaje. En 1966 recibió la medalla Fields por sus aportaciones al álgebra geométrica. Pero el problema era que este nuevo lenguaje era complejo y difícil de aprender. [ver Comparaciones – MENTAL vs. La Matemática Generalista de Grothendieck.]
Alain Coones ha creado un lenguaje totalmente nuevo para la comprensión de la geometría. Su geometría no conmutativa es una visión moderna de la vision riemanniana de la geometría que va más allá de la geometría de Weil y Grothendieck, revelando un mundo matemático completamente nuevo. Esta geometría ha demostrado ser un instrumento muy potente en su aplicación a la física cuántica, es especial para la teoría de cuerdas.
El lenguaje J
J es un potente lenguaje de programación que tuvo su apogeo en los años 1960’s. Fue diseñado por el mismo autor del APL, su antecesor, Kenneth E. Iverson [1995].
J es una notación matemática ejecutable. De hecho, Iverson ha escrito varios textos matemáticos utilizando J como notación.
J tiene una orientación semántica próxima al lenguaje natural. J consta de 70 verbos. Los verbos son funciones y se expresan con dos caracteres.
Iverson pretendía integrar la matemática y la informática, pero tiene el inconveniente de que requiere mucho tiempo de aprendizaje (por el excesivo número de verbos) y porque la notación llega a ser bastante críptica.
Frente a J, MENTAL solo requiere aprender 12 primitivas, y su notación siempre refleja claramente la semántica.
FMathL (Formal Mathematical Language)
FMathL es un proyecto de la Universidad de Viena de creación de un sistema (y un marco de trabajo) orientado a la formalización de problemas matemáticos y su tratamiento informático, incluyendo la demostración automática de teoremas. Sus características principales son:
- Separación completa entre los aspectos descriptivos y operativos.
- Utilización del lenguaje Z de especificación formal como medio para generar automáticamente el código fuente de un lenguaje de programación determinado. Z se basa en la teoría de conjuntos, el cálculo lambda y la lógica de primer orden.
- Utilización del “paradigma alfabetizado” (literate programming) de Donald Knuth. Este paradigma es una alternativa a la programación estructurada. Los programas se escriben de forma similar al lenguaje humano. El código Z se incluye en segundo plano.
- Utilización del lenguaje LaTeX para representar expresiones matemáticas.
- Generación automática de la documentación.
Bibliografía
- Cajori, Florian. A History of Mathematical Notations. Dover Books on Mathematics, 2011.
- Changeux, Jean Pierre; Connes, Alain. Materia de reflexión. Tusquets, 1993.
- Crosland, Maurice. The Language of Science. From the Vernacular to the Technical. The Lutterworth Press, 2006.
- De Cruz, Helen; De Smedt, Johan. Mathematical symbols as epistemic actions. Internet.
- De Cruz, Helen. Mathematical symbols as epistemic actions – an extended mind perspective. Internet.
- Guénon, René. Observaciones acerca de la notación matemática. La Gnose, 1910. Disponible online.
- Iverson, Kenneth E. J. Introduction and Dictionary.Iverson Software, 1995.
- Mazar, Joseph. Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers. Princeton University Press, 2014.
- O’Halloran, Kay. Mathematical Discourse: Language, Symbolism and Visual Images. Bloomsbury Academic, 2008.
- Scheinerman, Edward R. Mathematical Notation: A Guide for Engineers and Scientists. CreateSpace Independent Publishing Platform, 2011.